検巕壔妛偱偼丄僥僗僩慜偵夁嫀栤丄夁嫀墘廗栤戣丄崱婜墘廗栤戣偑攝晍傑偨偼巙揷嫵姱巜掕偺僀儞僞乕僱僢僩忋偵偰岞奐偝傟傑偡丅
偙偙偱偼2005-2007偺墘廗栤戣丒夁嫀栤椉曽傪採帵偟偰偍偒傑偡丅
島媊撪梕偼僋僜傒偨偂偵棟夝晄擻偱偡偑丄僲乕僩偺傒帩偪崬傒壜側偺偱梊傔帒椏傪嶌偭偰偍偔偲椙偄偱偟傚偆丅
仠検巕壔妛丂2007丂嘦晹丂巙揷嫵姱丂婜枛帋尡
丂侾丏揹巕偺敪尒偐傜儃乕傾偺悈慺尨巕柾宆偑採埬偝傟傞傑偱偺尨巕丒暘巕偺壔妛偺敪揥偺楌巎乮慜婜検巕榑乯傪丄
丂丂丂帺暘側傝偵梫栺偣傛丅
丂俀丏俙侕偲俛侕傪僄儖儈乕僩墘嶼巕偲偟偨帪丄俙侕俛侕丂亄丂俛侕俙侕偑僄儖儈乕僩墘嶼巕偲側傞帠傪帵偣丅
丂俁丏1師尦偺敔偺拞偵暵偠崬傔傜傟偨帺桼棻巕偺検巕椡妛揑僄僱儖僊乕弨埵偲攇摦娭悢偼丄
丂丂丂壓恾偺傛偆偵梌偊傜傟傞丅偙偺帪丄埲壓偺栤偄偵摎偊傛丅
丂丂丂丂丂丂
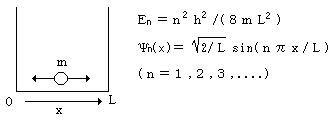
丂丂丂乮1乯戞堦椼婲忬懺偺棻巕偺埵抲偺懚嵼妋棪偼偳偆側傞偐丅恾乮僌儔僼乯偱昞偣丅
丂丂丂乮2乯婎掙忬懺乮値亖1乯偵偍偗傞塣摦検俀忔偺婜懸抣亙俹侕俀亜傪媮傔傛丅
丂係丏偦傟偧傟偺婰弎偑娫堘偭偰偄傞偺側傜棟桼偱巜揈偣傛丅
丂丂丂乮1乯悈慺尨巕偺帠偲偐
丂丂丂丂丂丂丂丂丂丂丂丂偡偂傑偣傫丅帒椏晄懌僨僗丅屻彫栤俁偮偲戝栤侾偮偁偭偨偲巚傢傟傑偡丅
仠検巕壔妛丂2007丂嘦晹丂巙揷嫵姱丂墘廗栤戣
丂侾丏揹巕偺敪尒偐傜儃乕傾偺悈慺尨巕柾宆偑採埬偝傟傞傑偱偺尨巕丒暘巕偺壔妛偺敪揥偺楌巎乮慜婜検巕榑乯傪丄
丂丂丂帺暘側傝偵梫栺偣傛丅
丂俀丏俙侕偲俛侕傪僄儖儈乕僩墘嶼巕偲偟偨帪丄俙侕俛侕丂亄丂俛侕俙侕偑僄儖儈乕僩墘嶼巕偲側傞帠傪帵偣丅
丂俁丏帪娫傪娷傑側偄Schrodinnger曽掱幃偼丄師偺條偵昞偝傟傞丟丂俫侕兊亖俤兊
丂丂丂偙偺帪丄俫侕丄兊丄俤偼偦傟偧傟壗傪昞偟偰偄傞偺偐丅傑偨兊俀偺帩偮丄暔棟揑側堄枴傪娙扨偵愢柧偣傛丅
丂係丏挿偝俴偺侾師尦偺敔偵暵偠崬傔傜傟偨幙検倣偺棻巕偺塣摦傪峫偊傞丅
丂丂丂乮1乯塣摦検偺婜懸抣傪媮傔傛丅
丂丂丂乮2乯塣摦検偺俀忔偺婜懸抣偺応崌偼偳偆偐丅
丂丂丂乮3乯塣摦検偺婜懸抣偺俀忔偼丄塣摦検俀忔偺婜懸抣偵堦抳偡傞偐丠丂傕偟堦抳偟側偄応崌偵偼丄偦偺棟桼傪峫偊傛丅
丂俆丏師偺岅嬪偺撪梕傪娙扨偵愢柧偣傛丅
丂丂丂乮1乯婳摴嬤帡
丂丂丂乮2乯僷僂儕偺尨棟
丂丂丂乮3乯揹巕僗僺儞
丂丂丂乮4乯Born-Oppenheimer嬤帡
丂丂丂乮5乯LCA0-MO
仠検巕壔妛丂2006丂嘦晹丂巙揷嫵姱丂婜枛帋尡
丂侾丏慜婜検巕榑偵娭偟偰丄埲壓偺栤偄偵摎偊傛丅
丂丂丂乮1乯悈慺尨巕偵崅揹埑傪偐偗傞偲丄婔偮偐偺摿掕偺攇挿偺岝傪敪偡傞丅偙偺寢壥傪Planck偺壖愢傪梡偄偰愢柧偣傛丅
丂丂丂乮2乯Bohr偺悈慺尨巕柾宆偺拞偵偼丄揹巕偺帩偮攇摦惈偑撪曪偝傟偰偄傞丅偙偺攇摦惈傪愢柧偣傛丅
丂俀丏墘嶼巕偵娭偟偰埲壓偺栤偵摎偊傛丅
丂丂丂乮1乯俙侕偲俛侕傪僄儖儈乕僩墘嶼巕偲偟偨帪丄俙侕値俛侕丂亄丂俛侕俙侕値丂偑僄儖儈乕僩墘嶼巕偱偁傞偙偲傪帵偣丅
丂丂丂乮2乯師偺娭悢偺拞偱丄墘嶼巕偺倓/倓倶偺屌桳娭悢偵側偭偰偄傞偺偼偳傟偐丅
丂丂丂丂乮a乯倕倝倠倶
丂丂丂丂乮b乯cos(倠倶)
丂丂丂丂乮c乯倠
丂丂丂丂乮d乯倠倶俀
丂俁丏懡揹巕尨巕偺揹巕攝抲偵偍偄偰丄倱婳摴乮侾s,俀s,俁s....乯偵偼嵟戝俀屄傑偱丄倫婳摴乮俀p,俁p,係p....乯偵偼嵟戝俇屄傑偱丄
丂丂丂倓婳摴乮俁d,係d....乯偵偼嵟戝10屄傑偱偺揹巕傪廂梕偡傞偙偲偑偱偒傞丅
丂丂丂偙偺巇慻傒傪丄検巕悢丄婳摴嬤帡丄揹巕僗僺儞丄僷僂儕偺尨棟傪梡偄偰愢柧偣傛丅
丂係丏1師尦偺敔偺拞偵暵偠崬傔傜傟偨帺桼棻巕偺検巕椡妛揑僄僱儖僊乕弨埵偲攇摦娭悢偼丄壓恾偺傛偆偵梌偊傜傟傞丅
丂丂丂偙偺帪丄埲壓偺栤偄偵摎偊傛丅
丂丂丂丂丂丂丂
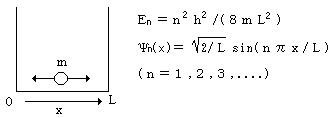
丂丂丂乮1乯戞堦椼婲忬懺乮値亖俀乯偵偍偄偰丄帺桼棻巕偑侽乣侾/俁俴偺椞堟偵懚嵼偡傞妋棪傪媮傔傛丅
丂丂丂乮2乯検巕椡妛偼婔偮偐偺嬌尷偵偍偄偰屆揟椡妛偺寢壥偵堦抳偡傞丅師偺俀偮偺嬌尷偱偼丄偳偺傛偆側寢壥偑摼傜傟傞偐丅
丂丂丂丂乮a乯帺桼棻巕偺僄僱儖僊乕偑旕忢偵戝偒側応崌
丂丂丂丂乮b乯帺桼棻巕偺幙検偑旕忢偵戝偒側応崌
仠検巕壔妛丂2006丂嘦晹丂巙揷嫵姱丂墘廗栤戣
丂侾丏揹巕偺敪尒偐傜儃乕傾偺悈慺尨巕柾宆偑採埬偝傟傞傑偱偺尨巕丒暘巕偺壔妛偺敪揥偺楌巎乮慜婜検巕榑乯傪丄
丂丂丂埲壓偺僉乕儚乕僪傪梡偄偰梫栺偣傛丅
丂丂丂丂丒Plucker摍偺曻揹娗偺幚尡
丂丂丂丂丒Rutherford偺尨巕柾宆
丂丂丂丂丒Planck偺壖愢
丂丂丂丂丒Bohr偺悈慺尨巕柾宆
丂俀丏俙侕偲俛侕傪僄儖儈乕僩墘嶼巕偲偟偨帪丄師偺栤偄偵摎偊傛丅丂丂
丂丂丂乮1乯俙侕丂亄丂俛侕丂偑僄儖儈乕僩墘嶼巕偱偁傞偙偲傪帵偣丅丂丂
丂丂丂乮2乯俙侕値丂乷値亖俀,俁,係....乸偑僄儖儈乕僩墘嶼巕偲側傞偙偲傪帵偣丅
丂俁丏1師尦偺敔偺拞偵暵偠崬傔傜傟偨帺桼棻巕偺検巕椡妛揑僄僱儖僊乕弨埵偲攇摦娭悢偼丄壓恾偺傛偆偵梌偊傜傟傞丅
丂丂丂偙偺帪丄婎掙忬懺偵偍偗傞棻巕偑侽乣侾/俁俴偺椞堟偵懚嵼偡傞妋棪傪媮傔傛丅
丂丂丂丂丂丂丂
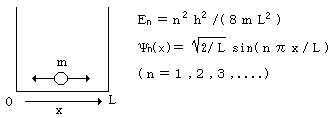
丂係丏師偺娭悢偺拞偱丄墘嶼巕偺倓俀/倓倶俀偺屌桳娭悢偵側偭偰偄傞偺偼偳傟偐丅
丂丂丂乮a乯倕倝倠倶
丂丂丂乮b乯cos(倠倶)亄倝sin(倠倶)
丂丂丂乮c乯倠倶
丂丂丂乮d乯倠倶俀
丂俆丏侾俽,俀俽,俀俹偲偼偳偺傛偆側尨巕婳摴偐丅抦傞強傪婰偣丅
丂俇丏峔惉尨棟偺婎慴偲側傞師偺俁偮偺撪梕傪娙扨偵愢柧偣傛丅
丂丂丂乮1乯揹巕僗僺儞
丂丂丂乮2乯僷僂儕偺尨棟
丂丂丂乮3乯婳摴嬤帡
丂俈丏暘巕婳摴傪峫偊傞偲偒偺婎慴偲側傞師偺俁偮偺撪梕傪娙扨偵愢柧偣傛丅
丂丂丂乮1乯Born-Oppenheimer嬤帡
丂丂丂乮2乯LCAO-MO
丂丂丂乮3乯曄暘尨棟
仠検巕壔妛丂2005丂嘦晹丂巙揷嫵姱丂婜枛帋尡
丂侾丏揹巕偺敪尒偐傜儃乕傾偺悈慺尨巕柾宆偑採埬偝傟傞傑偱偺尨巕丒暘巕偺壔妛偺敪揥偺楌巎乮慜婜検巕榑乯傪丄
丂丂埲壓偺僉乕儚乕僪傪梡偄偰梫栺偣傛丅
丂丂丂丂丒Plucker摍偺曻揹娗偺幚尡
丂丂丂丂丒Rutherford偺尨巕柾宆
丂丂丂丂丒Planck偺壖愢
丂丂丂丂丒Bohr偺悈慺尨巕柾宆
丂俀丏俙侕偲俛侕傪僄儖儈乕僩墘嶼巕偲偟偨帪丄師偺栤偄偵摎偊傛丅丂丂
丂丂丂乮1乯俙侕丂亄丂俛侕丂偑僄儖儈乕僩墘嶼巕偱偁傞偙偲傪帵偣丅丂丂
丂丂丂乮2乯俙侕俛侕亄俛侕俙侕偑僄儖儈乕僩墘嶼巕偲側傞偙偲傪帵偣丅
丂俁丏暘巕婳摴朄偺拞偵偼丄條乆側奣擮傗嬤帡朄偑摫擖偝傟偰偄傞丅埲壓偵帵偡奣擮傗嬤帡朄傪愢柧偣傛丅
丂丂丂乮1乯攇摦娭悢偺婯奿捈岎忦審
丂丂丂乮2乯曄暘尨棟
丂丂丂乮3乯俴俠俙俷-俵俷乮Linear Combination of Atomic Orbital亅Molecular Orbital乯
丂丂丂乮4乯僷僂儕偺尨棟
丂係丏1師尦偺敔偺拞偵暵偠崬傔傜傟偨帺桼棻巕偺検巕椡妛揑僄僱儖僊乕弨埵偲攇摦娭悢偼丄壓恾偺傛偆偵梌偊傜傟傞丅
丂丂丂偙偺帪丄師偺栤偵摎偊傛丅
丂丂丂丂丂丂丂
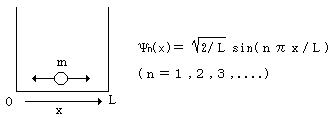
丂丂丂乮1乯戞堦椼婲忬懺偺棻巕偺埵抲偺懚嵼妋棪偼偳偆側傞偐丅恾乮僌儔僼乯偱昞偣丅
丂丂丂乮2乯偙偺儌僨儖宯偵偍偗傞乬儃乕傾偺検巕壔忦審乭偼丄埲壓偺傛偆偵梌偊傜傟傞丅偙偺棟桼傪峫偊偰傒傛丅
丂丂丂丂丂丂丂丂乮俀俴乯俹亖値倛丂乮値亖侾,俀,俁....乯
丂丂丂乮3乯棻巕偺慡僄僱儖僊乕偼塣摦僄僱儖僊乕偵摍偟偄偺偱埲壓偺傛偆偵梌偊傜傟傞丅
丂丂丂丂丂丂偙偺幃偲乮俀乯偺乬儃乕傾偺検巕壔忦審乭傪慻傒崌傢偣丄検巕椡妛揑僄僱儖僊乕弨埵偺昞幃傪媮傔傛丅
丂丂丂丂丂丂丂丂丂俤亖侾/俀倣倴俀亖俹俀/俀倣
仠検巕壔妛丂2005丂嘦晹丂巙揷嫵姱丂墘廗栤戣
丂侾丏揹巕偺敪尒偐傜儃乕傾偺悈慺尨巕柾宆偑採埬偝傟傞傑偱偺尨巕丒暘巕偺壔妛偺敪揥偺楌巎乮慜婜検巕榑乯傪丄
丂丂丂埲壓偺僉乕儚乕僪傪梡偄偰梫栺偣傛丅
丂丂丂丂丂丒Plucker摍偺曻揹娗偺幚尡
丂丂丂丂丂丒Rutherford偺尨巕柾宆
丂丂丂丂丂丒Planck偺壖愢
丂丂丂丂丂丒Bohr偺悈慺尨巕柾宆
丂俀丏俙侕偲俛侕傪僄儖儈乕僩墘嶼巕偲偟偨帪丄師偺栤偄偵摎偊傛丅丂丂
丂丂丂乮1乯俙侕丂亄丂俛侕丂偑僄儖儈乕僩墘嶼巕偱偁傞偙偲傪帵偣丅丂丂
丂丂丂乮2乯乥俙侕,俛侕乥亖俙侕俛侕亅俛侕俙侕傪俙侕偲俛侕偲偺岎姺巕偲偄偆丅
丂丂丂丂偙傟偑侽偺帪偺傒丄俙侕俛侕丂偑僄儖儈乕僩墘嶼巕偵側傞偙偲傪帵偣丅
丂俁丏帪娫傪娷傑側偄Schrodinnger曽掱幃偼丄師偺條偵昞偝傟傞丟丂俫侕兊亖俤兊
丂丂丂乮1乯俫侕丄兊丄俤偼偦傟偧傟壗傪昞偟偰偄傞偺偐丅傑偨兊俀偺帩偮丄暔棟揑側堄枴傪娙扨偵愢柧偣傛丅
丂丂丂乮2乯偙偺曽掱幃偼屌桳抣曽掱幃偺侾偮偱偁傞丅師偺娭悢偺拞偱丄墘嶼巕乮倓俀乛倓倶俀乯偺屌桳娭悢偵側偭偰偄傞傕偺偼偳傟偐丅
丂丂丂丂乮a乯倕倝倠倶丂丂丂乮b乯們倧倱(倠倶)丂丂丂乮c乯倠丂丂丂乮d乯倠倶俀
丂係丏俛尨巕乮儂僂慺尨巕乯偺婎掙忬懺偺揹巕攝抲偼丄乮1倱乯俀乮2倱乯俀乮2倫乯侾偲梌偊傜傟偰偄傞丅
丂丂丂乮1乯1倱丄2倱丄2倫偲偼偳傫側婳摴乮攇摦娭悢乯偐丅抦傞強傪婰偣丅
丂丂丂乮2乯俛尨巕偑偙偺傛偆側揹巕攝抲傪庢傞傢偗傪娙扨偵愢柧偣傛丅
丂俆丏師偺岅嬪偺撪梕傪愢柧偣傛丅
丂丂丂乮1乯揹巕僗僺儞
丂丂丂乮2乯僷僂儕偺尨棟
丂丂丂乮3乯婳摴嬤帡
丂丂丂乮4乯Born-Oppenheimer嬤帡
丂丂丂乮5乯LCA0-MO
丂丂丂乮6乯曄暘尨棟